- kaboo a écrit:
- Rappel :
21 janvier 2020 6 décès.
22 janvier 2020 9 décès.
23 janvier 2020 17 décès.
26 janvier 2020 56 décès.
28 janvier 2020 106 décès.
29 janvier 2020 132 décès.
30 janvier 2020 171 décès. (19 h 41 heure de Paris).
30 janvier 2020 212 décès. (23 h 55 heure de Paris).
Spectre a écrit l'équation 3x^2+2x+1 est le coronavirus.
Il pense que tes chiffres détermine des points géométrique. Il a du regarder l'allure de la courbe. Soit C(x) la fonction du coronavirus.
21 janvier 2020 6 décès, donc C(1,6)
22 janvier 2020 9 décès, donc C(2,9)
23 janvier 2020 17 décès, donc C(3,17)
26 janvier 2020 56 décès, donc C(6,56)
28 janvier 2020 106 décès, donc C(8,106)
29 janvier 2020 132 décès, donc C(9,132)
30 janvier 2020 212 décès. (23 h 55 heure de Paris), donc C(10,212)
Je l'ai fait pour vérifier. Spectre est un inconnu. Comment le contacter? Je lui écrit un message. On va faire sans lui.....
J'ai écrits que la courbe est une exponentielle.
- kaboo a écrit:
- Rappel :
21 janvier 2020 6 décès.
22 janvier 2020 9 décès.
23 janvier 2020 17 décès.
26 janvier 2020 56 décès.
28 janvier 2020 106 décès.
29 janvier 2020 132 décès.
30 janvier 2020 171 décès. (19 h 41 heure de Paris).
30 janvier 2020 212 décès. (23 h 55 heure de Paris).
le graphique est une exponentielle.

[/quote]
On remarque la coïncidence du début du coronavirus avec l'axe des abscisses:
21 janvier est le jour 1
22 janvier est le jour 2
23 janvier est le jour 3
etc
Il met dans son graphique en abscisse le nombre de jours: 0,1,2,3,....
Il met en axe des ordonnées le nombre de morts.
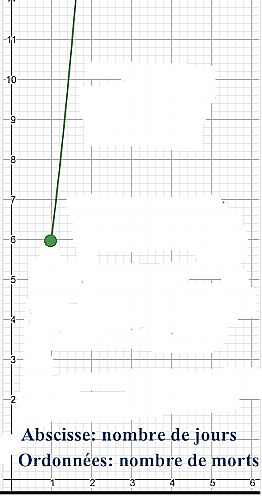
Spectre pense que c'est un polynôme du type
∑ [n=0] à [n=n+1](ax^(n+1)+bx(n)+c(n-1)+...+zIl a raison, il est plus précis que moi. Il y a plus de chance que ce soit un polynôme. Il faut déterminer son degré.
Quelle est la valeur de n?
Si n=1, on a ax^1+bx^0+c. On sait que x^0=1 (si x≠0).
Donc l'équation est de type ax+b qui est une droite. Les points indiquent presque une droite effectivement.
Si n=2 on a ax^2+bx+c. Il faut trouver les 3 inconnues a, b, c. On a besoin d'autant qu'équations, soit 3 équations. Spectre a pris 3 points qui se suivent dans cette série polynomiale selon la logique.
On prend les 3 premières coordonnées:
E(1,6), F(2,9), G(3,17). On a le système de 3 équations à 3 inconnues suivant:
a(1)^2+b(1)+c=6 E(1,6) que je simplifie:
a+b+c=6 E(1,6)
a(2)^2+b(2)+c=9 F(2,9) que je simplifie:
4a+2b+c=9 F(2,9)
La 3e équation est avec G(3,17):
a(3)^2+b(3)+c=17 que je simplifie:
9a+3b+c=17 G(3,17)
Soit à résoudre le système de 3 équations à 3 inconnues suivant:
a+b+c=6
4a+2b+c=9
9a+3b+c=17
J'utilise la méthode de Gauss.
La solution est unique et c'est:
a=645/2104
b=499/2104
c=141/1052
soit a=0,306..., b=0,237..., c=0,134...
En simplifiant on a:
a=0,3 b=0,2 c=0,1
Il a translaté de 10 pour avoir effectivement:
3x^2+2x+1=C(x)Spectre ne s'est pas trompé dans son estimation globale. Il est évident qu'en poursuivant, on affine l'équation polynomiale. Qui a envie de résoudre un système de 4 équations à 4 inconnues ??? :face: L'estimation est suffisante.
On aura un meilleur résultat avec une équation avec 10 inconnues. Spectre a estimé que pour se faire une idée dans le forum il en avait fait assez. Je le comprends.
Constat:1er jour 21 janvier 2020 6 décès: 3(1)^2+2(1)+1=3+3=6
ok2e jour 22 janvier 2020 9 décès: 3(2)^2+2(2)+1=3(4)+5=17
le résultat du 3e jour. C'est effectivement remarquable avec si peu de données puisqu'on en est au tout début!!!!
3e jour 23 janvier 2020 17 décès: 3(3)^2+2(3)+1=3(9)+7=34 :x
On vérifie avec d'autres points:
28 janvier 2020 106 décès, K(8,106)
29 janvier 2020 132 décès, L(9,132)
30 janvier 2020 212 décès, M(10,212)
Ce qui nous donne les 3 équations du second degré:
a(8]^2+8b+c=106 K(8,106)
a(9)^2+9b+c=132 L(9,132)
a(10)^2+10b+c+212 M(10,212)
soit à résoudre:
64a+8b+c=106
81a+9b+c=132
100a+10b+c=212
On obtient exactement la même solution S={645/2104;499/2104;141/1052}
⟺ S={0,3;0,2;01}
Par translation S=(3,2,1).
L'équation du coronavirus est toujours 3x^2+2x+1=ySpectre a raison, on aura quelques petites erreurs forcément parce qu'il a eu l'intuition que la courbe C du coronavirus est celle d'un polynôme C(x) sous la forme
3x²+2x+1=C(x)Je confirme que son graphique et ses conclusions sont largement estimables.
 Le 31 mars on aura environ 25 000 morts.
Le 31 mars on aura environ 25 000 morts. 